Avant-Propos:
Si vous avez suivi l'actualité du jeu vidéo, vous avez probablement entendu parler du rendu HDR, autrement traduit de manière barbare en français par rendu à grande gamme dynamique. Comme dans la phrase suivante : "La prochaine génération utilisera à fond le HDR, il y a aura du blooming et des lens flares et des effets de lumière par pixel". Pour la plupart des gens cela reste un beau charabia malgré l'importance que cela prendra bientôt dans le rendu des jeux en temps réel. Ce petit article tente de dédramatiser un peu tout cela en prenant appui sur la réalité™ pour démontrer/démonter ce qu'il est possible de faire et quels sont les ressources nécessaires. Je prends le point de vue du programmeur (le mien) ou de la personne qui n'est pas effrayée par la technique.
Il y a probablement beaucoup de bla blah déjà connu pour ceux qui sont familiers avec le sujet, mais j'espère apporter un point de vue un peu plus détaillé que ce qui est généralement fait.
Mère nature
Ce que l'on qualifie de manière globale par HDR est en fait une multitude de choses qui ne sont pas toujours bien comprises ou résumées par le terme. Tout d'abord il faut expliquer d'où cela vient : de la nature, du monde réel ce qui nous entoure quand on n'est pas devant notre écran cela s'entend. Dans la réalité la lumière a une poignée de caractèristiques qui font qu'elle n'est pas bien représentable par un écran d'ordinateur ou même sur une feuille de papier.
La première est son intensité ou plus exactement la dynamique de son intensité. Dit simplement, il n'y a pas d'intensité maximale dans la nature. (Et pas d'intensité minimale mais nous y reviendrons). Comment cela est-ce possible ? L'intensité est déterminée par la somme de l'énergie de photons qui composent un rayon lumineux et ces photons n'ont pas de frontières et peuvent cohabiter tranquilement dans un tout petit espace, diverger ou converger en un point unique. Bref il n'y a pas de limites à ce qui pourrait être sinon la luminosité maximale. Bien entendu votre oeil n'est pas équipé pour voir une intensité trop forte, ça le blesserait et on sait bien qu'une trop forte intensité de rayonnement électromagnétique quel qu'il soit peut vous tuer. Mais il y a de la marge. Comparez la lumière présente en plein jour et la lumière d'une bougie. La lumière en plein jour peut être 10000 fois plus importante que celle d'une pièce fermée, et votre oeil peut voir correctement dans les deux situations.
La deuxième est la précision avec laquelle varie cette intensité. Dans la nature on peut à une bonne approximation près considérer que l'intensité lumineuse varie de manière continue et non pas par palier. Ce qui est le contraire d'une représentation informatique sous forme de bits, même une représentation sous forme de nombre à virgule flottante que l'on détaillera ci-dessous varie par paliers - certes irréguliers. Là encore il y a une limite à ce que peut détecter notre vision, et nos représentations informatiques font tout pour exploiter la limitation de l'oeil.
L'écran et ses limitations
L'une des premières limitations de votre simulation de réalité par ordinateur est votre écran. La luminosité maximale de votre écran est très faible. Le seul endroit où il est utile c'est en intérieur à l'abri de sources de lumières trop fortes comme celle du soleil. Bien entendu il y a des écrans lumineux et d'autres moins lumineux, certains tolèrent une forte lumière ambiante et d'autres non (projecteurs). Mais cela reste incomparable par rapport à ce qui existe à l'extérieur. Il n'est pas encore question de risquer la cécité en regardant une page blanche sur votre écran d'ordinateur. Ensuite il y a une limite au rapport maximal entre le blanc et le noir de votre écran. Votre écran ne pourra jamais être totalement noir et plus vous augmentez la luminosité globale plus vous augmentez la luminosité du noir en contrepartie.

Si vous croyez que cet écran affiche du bleu, détrompez-vous. Il est en train d'afficher un écran noir, pris sans trucage avec mon appareil photo numérique. La lumière provient principalement de la lumière résiduelle qui vient du bombardement même avec tous les pixels éteints de la couche phosphorée de l'écran, un petit peu de l'environnement sous forme de réflexion et de diffusion. Si j'étais en plein soleil, la partie de la lumière provenant de l'environnement serait bien plus grande. J'ai mis une feuille de papier blanche à côté pour comparaison. La feuille de papier n'est éclairée que par l'environnement.
Un problème de bits
Le deuxième problème sans doute aussi sérieux est la quantité de détails que peut représenter votre écran ou votre carte graphique. On a évoqué plus haut le problème du contraste sur écran, en pratique il est illusoire de vouloir représenter de larges contrastes ou des variations infimes d'intensité parce que ni votre écran ni votre oeil ne pourront faire la différence. La plupart des affichages actuels se font donc avec un total de 8 bits pour représenter l'intensité lumineuse ce qui est peu mais tient compte des limitations de votre écran. Avec un très bon affichage on pourrait pousser à 10 bits mais au delà il y aurait un gachis d'information. Certains écrans sont tellement mauvais (la plupart des écrans LCDs) qu'ils ne peuvent varier leur intensité que sur une échelle de 7 ou 6 bits par canal, ils s'en sortent à peu près en faisant du dithering spatial ou temporel (on y reviendra).
Toutes ces limitations font qu'il est à peu près illusoire de vouloir représenter de manière aussi riche la réalité sur votre écran d'ordinateur.
L'effet que l'on cherche à obtenir c'est de faire passer un gros camion à travers un tunnel trop étroit. Ça ne passera pas sans faire quelques concessions.
Un problème ? Quel problème ?
On n'est pas toujours conscients des concessions que l'on fait surtout lorsque le choix a été imposé indirectement par la technique, ou si l'on est tellement habitué au compromis actuel qu'on ignore qu'il s'agit d'une représentation imparfaite.
Pour être clair, les compromis actuels de représentation de la réalité font qu'en restant devant son ordinateur on utilise moins d'un millième des capacités de notre vision. Plutot que des longs discours, je vais illustrer la flexibilité de l'oeil par un exemple. Il suffit de prendre une scène de la vie de tous les jours, comme l'observation du monde extérieur par votre fenêtre. Mon appareil photographique et votre écran d'ordinateur n'ont pas la flexibilité de votre oeil donc ce qui suit illustre très bien les grands contrastes existant dans la réalité.

Sur cette première photo, seul l'extérieur est visible. Les arbres sont éclairés directement par le soleil, le ciel est lui-même une source de lumière importante mais sa lumière provient du soleil donc comme source secondaire il ne peut pas éclairer autant que la source primaire (il y a quelques exceptions à ce fait, lorsque la source secondaire concentre les rayons de la source primaire mais ce n'est pas le cas ici). L'intérieur de la chambre, la lampe et le mur en bois sont uniformément noirs.

La deuxième photo est au même endroit, même moment mais en indiquant à l'appareil photo que les détails intéressants se trouvent dans les zones sombres. À ce moment là, le ciel apparait uniformément blanc, ainsi que les arbres et les maisons à l'extérieur. Par contre on voit très bien le mur en bois, la lampe était en fait constituée d'une partie noire et une partie blanche translucide et le mur de la chambre était blanc. Il est important de noter que aucune des parties de la scène n'est éclairée par la lumière principale (le soleil) mais par des lumières secondaires ou tertiaires (etc). C'est ce qui explique que l'intensité soit si faible, à chaque rebond du photon une grosse partie est absorbée et le reste est renvoyé dans toutes les directions.
Le soleil ne rentre pas dans ma chambre, l'ouverture de ma fenêtre est petite et la lumière parvenant jusqu'à mon clavier a probablement rebondi des milliers de fois et une bonne partie en a été absorbée. Pourtant je n'ai pas de problème à voir les lettres sur les touches et je peux voir le bleu du ciel en même temps par ma fenêtre. Oui mon oeil est flexible à ce point là. Tous n'ont pas cette chance.
Compression
Allons sortons les grands mots. Le problème du HDR tel qu'exposé jusqu'ici est principalement un problème de compression. Compression destructive qui plus est. Imaginez un enregistrement sonore depuis un CD, vous le comprimez au format mp3, le compresseur décide qu'il y a des détails que vous n'entendrez pas et les supprime pour réduire la taille de votre fichier. Ici c'est pareil, on a un signal d'origine dont l'intensité n'est pas bornée et de précision infinie. Le tuyau par lequel il peut passer ne permet que 256 valeurs possibles à espacement fixes. Et une intensité maximale relativement faible. Le tuyau ou représentation en question est aussi appelé low dynamic range, LDR - par opposition à HDR bien entendu. Le problème principal ici n'est pas celui du stockage contrairement au MP3 mais principalement du à la faiblesse du médium de reproduction. Il y a donc bien compression mais ça s'arrête là, on ne revient pas au message original, pas de décompression.
Quels résultats miracles peut donc apporter cette compression ? Je vais vous faire une révélation choc mais les deux photos de ma fenêtre prises ci-dessus utilisent une forme relativement avancée de compression. L'appareil sait que j'afficherai la photo sur mon écran, il doit donc décider (avec mon aide) où conserver des détails. En réalité il n'y aura pas de miracle, il faudra sacrifier du détail et pas qu'un peu..
Le processus de compression de HDR en LDR est aussi appelé Tone map (carte de teintes), puisque d'une certaine façon on classe des régions d'intensité ou de teintes dans un index à nombre limité d'entrées (carte). Je vais détailler les méthodes les plus couramment utilisées.
Saturation
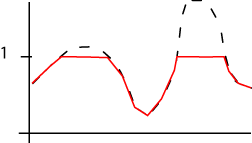
Vous êtes probablement comme Monsieur Jourdain pour sa prose, vous saturez sans le savoir. Le phènomène de saturation arrive dès que deux valeurs différentes deviennent indistinctes après le processus de compression. C'est à dire, deux valeurs proches de zéro deviennent zéro, ou encore deux valeurs supérieures à 255 deviennent 255. Si vous capturez la réalité ou que vous la simulez et si vous n'appliquez pas de contre mesure avant de comprimer alors la saturation peut finir par être très présente dans votre image finale et le résultat n'est généralement pas plaisant à l'oeil.
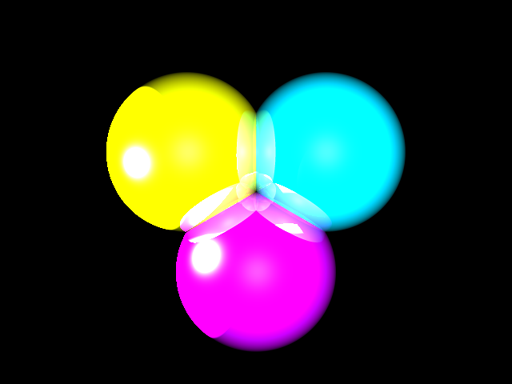
Je reprends de manière éhontée les illustrations de ma série d'articles sur le raytracing. L'image ci-dessus comporte des régions de forte intensité qui ont été rapportées à la valeur d'intensité maximale (255) ce qui fait qu'on ne perçoit plus aucun détail dans ces régions. Bien entendu, l'effet ici est forcé puisqu'il n'y a pas de détails visibles ailleurs. Mais le problème peut se poser par exemple dans un jeu, lorsque le rendu de la lumière est fixe et on ne fait pas de mise à l'échelle (voir ci dessous), dans ce cas, comme l'intensité lumineuse croit très fort près des sources ponctuelles, de la saturation autour de ces sources de lumières arrive fréquemment. Ce qui détruit toute forme de détails dans cette zone comme sur cette image.
Malgré ces inconvénients, cela est la principale méthode utilisée dans le jeu vidéo jusqu'à présent pour rendre les sources de lumières. L'opérateur de saturation est gratuit, on va dire qu'il vient par défaut avec les opérations de rendu des cartes graphiques et donc est une solution bon marché présente partout mais qui ne marche pas vraiment. Enfin ne peignons pas un tableau trop noir, elle marche relativement dans les univers très controlés des jeux vidéos où les artistes vont adapter la luminosité de chaque lampe et retravailler les textures et les couleurs pour qu'il n'y ait pas de saturation visible. Seuls les blockbusters comme Half Life 2 peuvent se permettre ce travail à fond et il est très coûteux. Si l'on veut un univers un peu plus réaliste il faut rajouter de l'adaptation, pour faire honneur à la partie dynamique du high dynamic range.
Mise à l'échelle. Transformation affine
La première solution qui vient à l'esprit quand on parle d'adaptation, c'est la transformation affine. C'est l'opération la plus simple qu'on puisse réaliser après la saturation toute simple. Si on veut éviter totalement les effets de la saturation, on doit détecter la valeur maximale sur l'image courante. Puis tout mettre à l'échelle en divisant par cette valeur maximale. On aura en prime la garantie que l'image ne sera pas totalement sombre, puisque cela marche aussi dans l'autre sens, en s'assurant que l'image finale LDR compressée utilisera la totalité de son domaine de valeurs. Dans un rendu animé où l'intensité varie d'une image à l'autre, on peut ainsi rendre compte des capacités d'adaptation de l'oeil humain aux hautes intensités et basses intensités tout en conservant une vue parfaite.
Hmm parfaite ? Pas tout à fait. L'un des problèmes qui apparait assez rapidement est que cette adaptation est uniforme sur l'intervalle [0, Imax] ce qui est bon si le détail à représenter est uniformément réparti dans cet intervalle mais il se peut très bien que Imax n'est atteint qu'à un endroit ponctuel (source de lumière) et que le reste de la scène soit plutot 200 fois moins lumineux. En ne faisant pas attention on se retrouve avec un unique point blanc et le reste de l'image toute noire. Ne croyez pas que ce soit un cas pathologique. Là encore, sauf si l'on est dans un univers très controlé, où l'on maitrise tous les paramètres du rendu, intensité des lumières position et couleurs des objets etc, et bien le résultat risque d'être une image bien trop sombre pour être utilisable, comme ci dessous.

L'ours en peluche est éclairé directement mais l'intensité lumineuse est simplement dix à vingt fois moindre que celle capturé au niveau du reflet spéculaire sur le pied de la lampe. On peut estimer ça facilement en calculant l'histogramme de l'image et en constatant que tous les pixels tendent vers le noir.
Plus facile à constater qu'à corriger, surtout avec un opérateur aussi simpliste il n'y a qu'un seul paramètre sur lequel on puisse jouer : le facteur de mise à l'échelle. En général il vaut tout simplement mieux calculer non pas la valeur maximale d'intensité mais l'intensité médiane ou la moyenne, selon la préférence et faire en sorte que cette valeur soit indexée en LDR par une valeur plus proche de 0,5. Mais on retombe dans le travers de l'opérateur de saturation. Les valeurs maximales ne sont plus bornées correctement et on a des artefacts liés à la saturation dans les hautes intensités. Cet opérateur n'a donc qu'une seule qualité: il est très peu cher, son coût est limité au calcul de l'intensité maximale ou médiane ce qui est peu en comparaison des opérateurs suivants. C'est plutôt à voir comme une introduction simple au problème d'adaptation dynamique du rendu HDR, mais ce faisant on perd toute possibilité de contrôle de la saturation qu'on avait dans un environnement statique, le remède peut paraître pire que le mal.
La demi vie
Non ce n'est pas une référence à Half Life mais une référence aux lois qui contrôlent les réactions chimiques. Une réaction chimique commence par la mise en présence de réactifs, lorsqu'ils se rencontrent ils donnent un produit et disparaissent. Généralement (sauf réaction en chaine), au fur et à mesure que les réactifs sont consommés, la réaction rallentit parce que les réactifs se font plus rares. À cause de ça une réaction non alimentée peut mettre du temps à atteindre son rendement maximal mais je m'éloigne du sujet. On peut modéliser une prise de photo comme cela, la lumière entre en contact avec un réactif, transformant le négatif en noir, la transformation est très rapide au début puis de plus en plus lente jusqu'à ce qu'elle soit proche de totale. Cela aboutit à une loi de conversion exponentielle où l'intensité lumineuse de plus en plus forte fait tendre la photo finale vers le blanc de plus en plus pur (une fois le négatif développé).
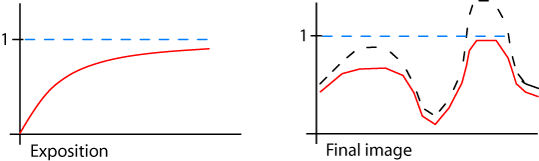
Cet opérateur exponentiel n'est pas seulement intéressant pour l'analogie avec la chimie ! En effet on constate que le résultat est naturellement borné, donc à priori pas besoin de calculer de valeur maximale pour éviter les "coupures" abruptes dans les hautes intensités. De plus l'image finale conserve une bonne dynamique dans les basses intensités. Enfin on peut controler finement le mapping de l'éclairement moyen avec un terme d'exposition, ce qui est donné par la fonction d'exposition suivante : 1 - exp(exposure * I).

Je reprends l'image de mes balles de ci-dessus avec exactement les mêmes conditions d'éclairage mais cette fois ci avec l'opérateur d'exposition simple détaillé ici. Le résultat est un peu plus plaisant à l'oeil, il a cependant fallu calculer l'intensité moyenne et faire une opération relativement lourde par pixel, calcul d'exponentiel. (cependant c'est toujours assez bon marché par rapport à ce qui va suivre).
Les sigmoïdes
Encore un gros mot, c'est une classe de fonction, appelée ainsi à cause de la forme de leur courbe en S. Il s'agit d'un rafinement de la fonction exponentielle utilisée ci-dessus. Le problème avec la fonction exponentielle était qu'on partait du principe que les détails les plus importants étaient dans les intensité basses ce qui peut être vrai pour une classe d'image mais pas toujours, et aussi parce que dans toute le domaine des intensités élevées, on se retrouve avec des teintes désaturées et qu'on n'a aucun contrôle là dessus. Le nombre de fonctions sigmoides qui pourrait nous intéresser est assez grand, pas la peine de toutes les énumérer.
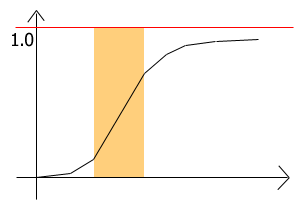
L'intérêt d'un tel opérateur est la zone en jaune, là où la réponse est quasi linéaire et le contraste est maximal. Avec un choix judicieux de paramètres il est donc possible de mettre en évidence une zone particulière d'intensité qui constituera le "noyau" de l'image finale. Dans cette zone, les couleurs sont presque fidèles, et le contraste fort de l'image original qui aurait pu être mangé par les opérateurs précédent est mieux conservé. L'une des raisons pour laquelle ce système peut marcher c'est grâce au SLC, simultaneous lightness contrast : l'oeil percevra le contraste plutôt que l'intensité réelle, même si la position sur l'échelle des intensités semble chamboulée, le contraste que l'on essaie de préserver jouera le rôle principal dans l'impression sur l'oeil et le cerveau. On peut encore pousser cela plus loin comme on va le voir dans la section suivante.
Opérateur local
Malgré ces efforts de préserver les détails dans une zone d'intensité particulière, parfois l'image que l'on veut afficher n'est pas constituée d'une seule zone intéressante mais de plusieurs zones intéressantes. et là les opérateurs globaux qu'on a utilisé jusqu'ici ont montré leur limite. Revenons à nos deux images du début. La photo de la chambre n'est pas si pathologique que cela, cela arrive fréquemment que sur une même image on ait une zone sombre et une zone éclairée, mon appareil qui n'est pas très sophistiqué ne peut concilier les deux et doit faire un choix ou un mauvais compromis (les deux zones peuvent paraitre délavées). Pourtant comme je l'ai dit notre oeil est parfaitement capable de voir les deux dans cette situation. Comment rendre ça ? Ça peut ressembler à la quadrature du cercle, j'ai un éléphant et une fourmi et je veux les voir tous les deux parfaitement sur une seule photo. En fait ce n'est pas si désespérant que cela du moins si on veut y mettre le prix. On peut à nouveau utiliser la propriété de notre oeil à voir principalement les contrastes plutôt que les intensités.

Les zones intéressantes occupent, certes, des parties de notre intervalle d'intensité très différentes mais elles sont également séparées spatialement. Le ciel très clair dont je veux les détails se trouve en haut de l'image. Le sol très sombre dont je veux les détails se trouve en bas de l'image. Il est donc envisageable de couper notre image en deux parties et d'appliquer la fonction sigmoïde sur chacune des parties pour préserver le maximum de contraste et de booster les couleurs. Mais comment réunir les deux parties sans que cela jure trop ? Problème qui peut sembler mal posé, insoluble puisqu'on risque au pire d'introduire des inversions de gradients : un objet peu lumineux adjacent à un objet très lumineux mais dont la représentation dans notre image compressée est inversée. Les solutions cependant existent et sont diverses et variées.
On peut par exemple, partir du principe que les grandes variations d'intensité perçues sont de basse fréquence (ce qui peut sembler le cas dans notre séparation haut bas) et que l'on peut extraire cette information, la compresser sans toucher aux gradients haute fréquence de notre image qui constitueront les détails précis que l'on ne veut pas perdre. Cela peut être fait par exemple, en recalculant les paramètres des opérateurs comme on le fait de manière globale mais cette fois ci en renouvelant le calcul pour chaque pixel et en travaillant sur une zone réduite de l'image (convolution par une gaussienne centrée sur le pixel par exemple). Faire un calcul de l'intensité moyenne par ce moyen, revient à prendre une version très basse fréquence de l'image ou de faire un flou gaussien sur l'intensité de départ.

Il y a un gros dégradé d'intensité entre le haut et le bas, mais comme il est réparti sur un grand espace et comme notre oeil est plus sensibles aux variations rapides (contrastes) qu'aux variations lentes, il peut assimiler une surface dégradée comme un aplat. Ensuite on utilise cette moyenne locale pour évaluer le paramètres de notre fonction de mapping. On peut avoir à renouveler le calcul plusieurs fois si l'on utilise plusieurs paramètres.

L'image précédente est une simple simulation "à la main" dans photoshop et n'utilise pas un vrai opérateur. On va dire que le résultat est plutôt heureux sur cette image, parce qu'effectivement il n'y a que deux zones bien définies et elle se prête bien à cette compression via flou gaussien. On pourrait critiquer le rendu des couleurs et des intensités locales mais au moins on a évité les effets de "halo". Un halo est quelquechose qui arrive fréquemment lorsqu'on travaille sur des images dont les grandes variations d'intensité sont moins bien localisées et séparées. Par exemple sur l'image suivante, on s'est intéressé d'un peu trop près aux détails des arbres qui sont sur la bordure entre les zones de haute intensité et celles de basse intensité. Si l'on avait utilisé un flou plus large on aurait alors sacrifié les détails présents dans les arbres mais évité le halo comme plus haut.

Heureusement il existe des opérateurs encore plus sophistiqués qui absorbent les grandes variations tout en préservant les détails locaux et ne rajoutent pas de halos malheureux. Je ne vais pas tous les citer mais il y a par exemple une compression dans le domaine du gradient qui travaille dans l'espace des gradients en atténuant ceux-ci juste ce qu'il faut pour compresser les intensités tout en préservant l'ordre. Ou encore le filtrage bilateral rapide qui va utiliser un flou mais en épargnant les contours pour limiter les halos. Voir le bas de la page pour les détails.
Fin de la première partie
Voilà on arrive à la fin de la première partie, j'espère que les explications ont été assez claires. Sinon n'hésitez pas
à m'envoyer un email à l'adresse : 
L'image suivante a été calculé avec un des opérateurs avancés, qui préserve les détails locaux. Il utilise une fonction de réponse sigmoïde ce qui permet de booster les contrastes et éviter de délaver les couleurs (le tout sans halo !). On peut même pousser les paramètres un peu plus loin et obtenir des rendus un peu surréalistes.

La suite traitera des problèmes plus spécifiques au rendu d'images HDR.
Direction page 2 : "Du rendu LDR au HDR".
En savoir plus (en anglais):
http://www.cs.ucf.edu/~reinhard/cdrom/ Photographic Tone Reproduction.
http://www.cs.huji.ac.il/~danix/hdr/ Gradient Domain HDR Compression.
http://people.csail.mit.edu/fredo/PUBLI/Siggraph2002 Fast Bilateral Filtering for HDR Images