Du Rendu LDR au HDR, High Dynamic Range

Ceci est la deuxième partie de mon article dédié au HDR, high dynamic range. La première partie contient l'introduction et la description d'opérateurs de tone mapping ou compression.

La synthèse en 8 bits ou LDR

Revenons un peu en arrière et intéressons nous aux jeux vidéos interactifs qui ont bercé notre enfance. Les jeux ont commencé en 2D ou en 3D filaire avec deux valeurs affichées noir et blanc. Puis ils ont progressé pour afficher de la couleur tout d'abord en peignant la couleur à même l'écran puis en modifiant le signal vidéo pour exploiter les capacités couleurs des télés. Au début il n'y avait que quatre couleurs, puis seize. Bien entendu il n'y avait pas de nuances, on arrivait à représenter des valeurs différentes par divers moyens comme le tramage ou l'utilisation de couleurs pour simuler des niveaux d'intensité. Puis on arrive à 4096, les nuances arrivent on arrive à représenter des photographies avec une fidélité toute relative. Après un bref passage à 65000 couleurs nous voici désormais aux 16 millions de couleurs représentables sur un écran et plus en exploitant le tramage et autres (à l'exception des écrans LCDs et projecteurs qui sont toujours limités de 60000 à 300000 couleurs mais qui simulent plus grâce au tramage). Les jeux ont toujours suivi (le plus souvent avec un temps de retard) les capacités d'affichage des machines et des écrans.

Si l'on atteint la capacité d'affichage de l'écran, ça veut dire qu'on peut s'arrêter, non ? C'est la réflexion qu'on peut souvent entendre lorsqu'on parle d'augmenter la charge de calcul pour rendre plus que ce que ne sont capables d'afficher nos écrans et nos cartes graphiques. En gros ça revient à ça : mon écran peut afficher 16 millions de couleurs, si j'affiche déjà un dégradé directement sur mon écran en 16 millions de couleurs, je ne verrai pas plus de détails en augmentant la résolution des couleurs. C'est vrai.. dans une certaine mesure et pour les images statiques uniquement.

Mais pour les jeux vidéos et la synthèse d'image c'est radicalement faux. Les problèmes qui se posent sont multiples, le premier problème c'est que si l'image finale est bien en 8 bits à précision fixe par canal de couleur, les calculs intérmédiaires s'ils sont faits uniquement dans cette représentation là perdront rapidement en précision. Comme les shaders et les éclairages sont de plus en plus nombreux et exigeants cela n'est plus acceptables. Et cela même si comme c'est souvent le cas, on est encore loin de la précision requise pour représenter la réalité. Et c'est le deuxième problème. Si l'on veut représenter des situations réalistes (y compris pour un rendu cartoon, il suffit de regarder the Incredibles et autres pour s'en rendre compte) alors nos 8 bits pour les calculs intermédiaires ne sont plus suffisants.

Exemple : la réflexion

La théière ci dessus est faiblement réflexive. On stocke une image de l'environnement dans une cubemap afin de la réutiliser plus tard pour simuler la réflexion. La partie droite de l'image stocke la partie intérmédiaire avec tous ses détails y compris les objets les plus lumineux. La partie gauche de l'image stocke dans l'espace de l'écran.

Bien entendu, l'exemple n'est pas forcément le meilleur puisque la reflexivité de la théière est constante et l'on aurait pu faire l'adaptation en amont pour continuer à utiliser un format huit bits proche de celui de l'écran. Cependant cet effort d'adapter en amont est faisable dans ce cas mais de plus en plus compliqué si en plus on a une réflexivité variable (style Fresnel), ou si on ajoute d'autres effets par dessus. Au moins utiliser un format intermédiaire qui contient plus de détails que le format de l'écran permet de voir clair et de ne pas compliquer trop le pipeline et les calculs.

Les formats intermédiaires

On a vu dans la première partie que dans le monde réel la quantité de lumière n'était pas bornée et avait une précision infinie. On n'a pas besoin d'autant de précision (si jamais c'était possible [grin]). Le calcul est simple.

C = A * B;

Si C est en précision 8 bits fixe (intervalle minimal entre deux valeurs 1/256), et si pour obtenir C on multiplie A par B, si A = 10 alors on peut se contenter de connaitre B avec une précision d'ordre 1/2560. De même si la valeur maximale de C est 1, que A = 1/10, alors on ne peut pas se permettre de tronquer avant B = 10 mais au delà de cette valeur c'est bon. Donc si par un heureux hasard on sait que A varie entre 1/10 et 10, alors on sait que l'on peut se limiter à un ensemble où B prendra 25600 valeurs entre 0 et 10.

C'est la représentation la plus simple que l'on puisse avoir, une représentation fixe qui peut être représenté sous forme d'entier 16 bits (double précision). On ne peut pas encore vraiment parler de HDR là, parce que c'est juste un peu meilleur que la représentation écran. On utilisera le terme de Wide Range (gamme élargie).

C'est un problème d'échelle, pour A qui varie entre 1/10 et 10, ça passe. Entre 1/100 et 100 ça ne passe plus On aurait besoin de 2.560.000 valeurs à précision fixe pour couvrir tous les cas possibles et un nombre à précision fixe de 16 bits ne suffit plus (en supposant qu'on ne veuille pas perdre de précision). Peut-on faire mieux ? Passons rapidement sur l'idée que l'on peut adapter B en amont si l'on connait suffisamment comment varie A. C'est peut-être faisable sur quelques exemples bien choisis mais ça ne nous donnera pas forcément la paix de l'esprit nécessaire. Par contre on peut se rendre compte de quelque chose. Si l'on a bien besoin pour B d'un intervalle de 1/25600 entre deux valeurs quand A vaut 100, ce n'est plus le cas lorsque A vaut 1/10. Parce que quand A vaudra 1/10, l'erreur sur B sera divisée à la place d'être multipliée. De même si l'on a bien besoin de représenter les nombres jusqu'à 100 lorsque A vaut 1/100, il n'en est pas de même lorsque A vaudra 10 parce que la valeur de B pour laquelle C saturera sera plus petite que 1.

Cette observation nous montre qu'il est possible d'utiliser au mieux ces 16 bits de précision en optant pour une autre représentation. Cette représentation est la représentation flottante. L'espace de représentation du flottant est très asymétrique. Avec une très grande précision pour les nombres petits. Et une précision plus faible pour les nombres grands mais en échange la possibilité de représenter de plus grands nombres qu'avec des entiers.

La représentation la plus courante jusqu'à présent dans les jeux temps réel qui tentent d'exploiter le HDR est le nombre demi-flottant. Aussi appelé half, half précision, fp16 (floating point 16 bits) ou encore OpenEXR parce que c'est la représentation choisie par ce format standard de fichiers.

Le nombre flottant diffère du nombre entier parce qu'il interprète ses bits de manière différente selon leur ordre. Les bits les plus bas représentent la mantisse. C'est la représentation "décimale" d'un nombre mais déclinée en binaire et rapportée à 1,XXX comme en notation scientifique. Les bits plus hauts représentent l'exposant. C'est le logarithme du nombre par lequel il faut multiplier la mantisse pour obtenir le nombre flottant que l'on veut représenter. Enfin le bit le plus haut est un bit de signe. On désigne souvent ces nombres sous forme s10e5, pour rappeler combien de bits sont dédiés à la mantisse (10), combien sont dédiés à l'exposant (e5) et qu'il y a un bit de signe (s). grâce à cette décomposition il est donc possible de représenter des nombres très petits avec grande précision et des nombres très grands mais avec une précision moindre. Ce qui n'est pas génant si l'on se contente d'opérations sous la forme C = A * B;

Quid de A ? On est parti du principe que A était de précision infinie, mais si l'on cherche à déterminer la précision nécessaire pour stocker A, alors on peut faire le raisonnement identique connaissant l'ordre de B puisque la formule A * B est symétrique.

En pratique cela ne suffira pas, toutes les opérations ne sont pas des multiplications, il y a des divisions, des soustractions, des racines carrées, des logarithmes et des exponentielles. Pour cette raison, il serait préférable de travailler avec une précision bien plus supérieure comme FP32, le format usuel utilisé par nos CPU pour les calculs flottants ou encore le FP64, le double de la précision tel qu'il est utilisé pour certains rendus haut de gamme (films de cinéma). Évidemment pour notre théière, half est largement suffisant, on aurait même pu se contenter d'entiers 16 bits (format wide range).

Les textures : le stockage

Si tous les hardwares modernes sont capables de traiter les opérations par pixel en 16 bits flottants ou 32 bits flottants en standard et sans surcoût, opter pour des textures dans ce format est encore très coûteux. Cas classique de la texture diffuse : cette texture représente l'albedo ou la quantité de lumière renvoyée par canal de couleur dans la direction de l'observateur. En théorie si on suit ce qui a été dit, il faudrait la stocker à très haute précision mais remplacer une texture 8 bits par canal compressé par une texture 32 bits par canal non compressé (les formats de compression pour les textures au format flottant ne sont pas encore légion) est extrêmement couteux. Le disque est saturé, la mémoire système est saturée et la mémoire vidéo est saturée. Un jeu moderne n'a aucun problème pour remplir 256MB de mémoire de texture en 8 bits par canal, inutile d'espérer la même quantité en passant tout au format HDR.

En pratique on est chanceux. La texture diffuse est encore celle qui est la plus utilisée (en passe d'être remplacée par la carte des normales et d'autres plus sioux encore). Et cette texture est généralement bornée et n'a pas besoin d'une grande précision du moins pour le stockage. On peut envisager des cas pathologiques (rampe linéaire sombre très largement amplifiée) mais c'est quelque chose sur lequel on peut avoir un certain contrôle (rajouter du dithering sur la texture) et il y a des contre mesures comme le fait que certaines cartes graphiques feront le filtrage bilinéaire pour la magnification à une précision supérieure à celle du stockage.

La texture qui a le plus de chance d'être rapidement convertie à des précisions supérieures est la texture d'environement. Qu'elle soit calculée à la volée comme pour l'exemple de la théière ou qu'elle soit stockée sur disque. Si l'on prend les FPS actuels, on voit que tous les écrans en extérieur utilisent une skybox (boîte centrée autour du joueur qui représente le ciel). Cette skybox dans le cas d'un jeu qui veut mimer la réalité doit avoir la même dynamique que la scène qu'elle entoure. Si l'on fait des calculs intermédiaires en 16 bits flottants avant d'appliquer un opérateur de tonemapping, alors cette skybox devra de même avoir une précision proche de ces 16 bits flottants.

Sur l'image précédente on a stockée notre skybox dans une cubemap au format ".hdr". Alors pour confondre tout le monde, ce format ".hdr" est un format un peu batard entre le LDR et le vrai HDR. C'est un format qui utilise 8 bits par canal, mais y adjoint un exposant global qui va multiplier les trois canaux rouge vert et bleu (RGBE, E pour exposant). En pratique ça marche relativement bien, ça ne prend pas plus de place qu'une texture au format RGBA (rouge vert bleu et couche alpha). Le seul problème étant que jusqu'à présent ce n'est pas un format natif pour les cartes graphiques et donc si vous voulez l'utiliser en temps réel il faudra faire la conversion par vous même à la lecture et à l'écriture dans un pixel shader.

Comme ce n'est pas un format natif, il ne peut utiliser les capacités précablées comme l'alpha blending et le filtrage de textures, et donc ne peut pas forcément être utilisé comme format de rendu principal (100% des jeux vidéo utilisent une forme de blending et 100% des jeux utilisent le filtrage de textures). C'est probablement le blending qui lui manque le plus. En plus du besoin de convertir en entrée et en sortie ce qui peut le rendre plus lent que d'autres formats plus directs. Pour le filtrage, un filtrage bilinéaire (pas anisotropique et pas trilinéaire..) peut être facilement émulé dans un pixel shader et au pire on peut appliquer le filtrage du pauvre en considérant E comme une couche alpha. Pourquoi ce n'est pas forcément pire que le vrai filtrage naturel ? c'est pour la suite.

Les textures : le filtrage

Le bât blesse dans ce domaine. On voudrait pouvoir contrôler finement la qualité de filtrage de nos textures pour tenir compte des traitements postérieurs comme le tonemapping mais en fait on est limité à ce que nous propose la carte graphique du moins si l'on veut une rapidité décente. Le filtrage actuel part du principe (intelligent dans la plupart des cas) qu'il y aura une correspondance linéaire entre la valeur lue depuis la texture et le pixel correspondant à l'écran. C'est le cas pour les textures diffuses qui même si elles subissent des multiplications par des lumières directes, des additions par des termes spéculaires, conservent un lien linéaire (affine) avec leur valeur d'origine. (C'est un peu moins vrai pour d'autres types de textures - normal map, shadowmap - mais ce problème n'est pas limité aux seuls rendus HDR). Enfin ceci jusqu'à l'heure de la conversion vers le format de l'écran, qui va compresser, saturer et probablement chambouler un peu notre texture

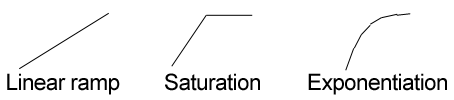
La non linéarité n'est pas un problème en soi.. En passant du HDR au LDR, on a implicitement abandonné la notion de conservation de l'énergie. Non le problème est que la linéarité est à la base du principe d'antialiasing des textures (et celui de la géométrie aussi. Le problème sera le même.). Pensez mipmapping, minification bilinéaire, anisotropie, summed area table, etc. L'antialiasing repose sur la possibilité d'établir une relation visuelle entre l'aire occupée et l'intensité perçue. En diminuant la résolution du quart, je devrais percevoir moins de détails mais je peux simuler la même perception des niveaux d'intensité en faisant la moyenne des couleurs sur un grand pixel pondérée par l'aire qu'ils occupaient originellement par petits pixels. En appliquant une transformation non linéaire à tout cela on obtiendra un rapport faussé entre l'aire originale et l'intensité perçue à l'écran, ce qui donnera un aspect de "corde" (roping) là où on devrait avoir un beau dégradé homogène. Voir l'image suivante agrandie cent fois pour l'illustration

L'aspect rugueux des bords lisses, les moirés (motifs géométriques qui n'existent qu'à cause d'un mauvais filtrage), les effets de clignotements d'une image à l'autre, voilà ce qui nous attends dans cette configuration. Pourtant, me direz-vous, ce modèle est bien meilleur que celui qui consiste à calculer la moyenne pondérée APRÈS le tone mapping, au moins un point très lumineux aura contribué plus à l'intensité finale qu'un point qui l'est moins. Oui et non. C'est certes le cas que si on a un point très lumineux dans les quatre qui contribuent à mon pixel, ce gros pixel devrait au final être très lumineux même si les trois autres sous-pixels sont noirs. Et faire le calcul avant le tonemapping garantit cela. Le problème est que cette réflexion est vraie dans un modèle continu, où le point contribue autant aux pixels adjacents qu'au sien, et qui plus est, il ne sature pas aux frontières de ce pixel (saturation physique, la contribution ne dépassera un certain carré). Mais notre façon de calculer la contribution des pixels, par un simple box filter sur les quatre sous-pixels que regroupe un gros pixel, ne permet pas de représenter cela correctement. On peut améliorer un tout petit peu en utilisant un noyau de convolution plus étendu, idéalement couvrant tout l'écran ou plus. En pratique on ne peut pas toujours faire ça (pas de contrôle de l'algorithme de filtrage, surcoût de la lecture des textures et ajout de flou). De plus cela contribue au "blooming" qui est la fuite des intensités fortes sur les pixels adjacents plus sombres et qui gomment certains détails visibles.

Si l'on utilisait un opérateur linéaire (même localement) on pourrait éviter une partie de ces problèmes (voir page précédente). Pour l'instant aucun de ces opérateurs "vraiment linéaire" n'est utilisé, soit parce qu'ils n'offrent pas une qualité suffisante, soit parce qu'ils sont trop couteux à mettre en oeuvre (et les opérateurs locaux avec détection des contours cassent leur linéarité aux contours pour ajouter à tout ça). Mais qui vivra verra.

Le tone mapping

Je vous ai alléché avec la page précédente et les opérateurs de tone mapping complexes. Pour le temps réel, on se contentera le plus souvent de mise à l'échelle avec saturation (contrôlée, au moins on essaie), ou d'opérateur non linéaire comme le fameux I/(1+I) qui est proche de la forme de l'exponentielle utilisée plus haut. La rapidité prime avant tout et surtout il faut être capable d'estimer les paramètres à chaque image, si possible sur le GPU pour éviter de casser le parallélisme.

Le problème du tone mapping est le même que celui de la profondeur de champ (depth of field) ou du flou du mouvement (motion blur). Si l'on utilise un terme global, on a intérêt à bien le choisir, les modèles calqués sur la photographie ne marchent que lorsque l'auteur (photographe) contrôle finement le sujet et tient les manettes. En environnement interactif, tant pis si l'on ne peut pas rendre tous les détails de l'image correctement ou si l'on se retrouve avec une image délavée. Voici sur ces deux images ce qui représente l'état de l'art en terme de tone mapping temps réel.

Simple mise à l'échelle avec saturation.

Opérateur "rationnel" de type I/I+1

Conclusion

Il y aurait encore beaucoup à dire sur le sujet et il y a beaucoup de techniques, de hacks, de théories derrière tout ça que toute une vie n'y suffirait pas. J'espère que cette introduction vous aura intéressé suffisamment pour vous pousser à regarder d'un peu plus près cette "révolution" annoncée. Et qu'elle vous permettra de comprendre et décrypter ce dont seront fait les jeux de demain .

Questions et commentaires à : LeGreg <>

Annexe I :

des problèmes avec vos flottants ? pensez aux nombres spéciaux

Les méthodes de travail hérité du temps où les nombres n'étaient que des entiers (ou nombres fixes) trouvent leur limite avec les nombres flottants. Par exemple, une carte graphique va traiter naturellement tout dépassement sur un nombre entier par une saturation (mise à 1 de toute ce qui est supérieur à 1, à zéro tout ce qui est inférieur à zéro). Cette notion de saturation gratuite disparait avec les flottants. Un nombre flottant peut-être négatif. Quel intérêt de représenter une couleur comme négative ? aucun mais c'est juste le format qui est comme ça, vous devez juste penser que ça peut arriver même par une erreur d'arrondi. De même si vous dépassez la valeur maximale, la carte graphique va mettre le nombre à l'infini. L'infini ? c'est presque comme la valeur max (MAX_INT) sauf que ça absorbe tout. infini - 1 = infini. infini/2 = infini. Et là où ça devient carrément lourd c'est infini * zéro = NaN (not a number). Et oui il y a un nombre qui n'est pas un nombre en représentation flottante (il y en a plusieurs en fait mais passons). Et NaN aussi absorbe tout : NaN + 1 = NaN, NaN / 2 = NaN. Pour s'en préserver il faut saturer soi meme. Si possible avant que ça n'arrive. Ou ajouter des controles sur les variables qui alimentent la carte graphique. +Inf pour les HALF float c'est tout nombre supérieur a 65500, facile d'y arriver si l'on n'a pas fait attention. Vous avez les mêmes problèmes sur les CPU (float IEEE), mais comme les nombres sont sur 32 bits ou 64 bits il faut aller beaucoup plus haut pour voir le problème survenir.

More articles and commentaries : Back to journal.